物理学习笔记1-角动量与转动惯量

本文大致难度：高中至强基

转动惯量导入

我们知道，力的定义如下：

$\vec{F}=m\vec{a}=m\frac{ {\rm d} \vec{v} }{ {\rm d} t }=\frac{ {\rm d} \vec{p} }{ {\rm d} t}$

（其中$F$是力。根据牛顿第二定律，$F=ma$，$m$为物体的质量，$a$为物体的加速度。$p$为动量，定义如$\vec{p}=m\vec{v}$。矢量物理量仅在本章打向量箭头，方便理解）

根据角动量的定义：

$\vec{L}=r\times \vec{p}=r\times (m\vec{v})$

（其中$L$为角动量）

显然可得：

$\frac{ {\rm d} \vec{L} }{ {\rm d} t}=\vec{M}=\vec{r}\times\vec{F}$

（其中$M$为力矩）

我们是否可以类比力的定义式子，用角加速度乘以一个东西定义力矩呢？显然可以。

$\vec{r}\times\vec{F}=I\vec{\beta}$

（其中$\beta$为角加速度）

我们需要定义一个新的物理量$I$。在力的定义式中，$m$的全称为“惯性质量”。那么我们可以称$I$为“转动惯性质量”，简称“转动惯量”。

转动惯量的定义式

根据上面的公式，我们可以得到：

$\frac{ {\rm d} L}{ {\rm d} t}=I\beta$

两边同时对时间积分：

$\int I\beta {\rm d} t=\int {\rm d} L$

可得：

$L=I\cdot\Delta\omega$

（其中$\Delta\omega$为角速度的变化量）

小绿本《物理竞赛教程（高中第一分册）》中的刚体力学那一章对转动惯量的定义原话如下：

转动惯量是描述刚体转动惯性大小的物理量。设刚体中质量元${\rm d}m$与转轴的距离为$r$，则刚体绕该轴转动时的转动惯量定义为$I=\int r^2 {\rm d}m$

刚体的转动惯量，既与刚体的质量及其分布情况有关，也与转轴的位置有关。设刚体的质量为$m$，则转动惯量可记为$I=mr_0^2$

其中$r_0$称为刚体的回旋半径。

根据我们计算得到的$L=I\cdot\Delta\omega$，我们可以尝试将其换一种形式表达：

$\begin{aligned} I&=\frac{L}{\Delta\omega} \\ &= \frac{rmv}{\frac{v}{r} }\\ &= mr^2 \end{aligned}$

由此可见，我们的计算是没有问题的。

那么动能的公式，我们可以推导成$I$和$\omega$的形式吗？当然可以！

$\begin{aligned} E_k&=\frac{1}{2}mv^2\\ &=\frac{1}{2}m(\omega R)^2\\ &=\frac{1}{2}I\omega^2 \end{aligned}$

物体转动惯量的计算

1. 质点的转动惯量

对于一个质量$m$的质点，与转轴的垂直距离为$r$时，根据定义式，其转动惯量$I=mr^2$

2. 棍棒的转动惯量

(1) 端点轴

对于一个质量为$m$，长度为$l$的密度均匀棍棒，围绕其一端点旋转。设其线密度$\lambda=\frac{m}{l}$，将其木棒分成许多长度为$\Delta r$的小块，每个距离转轴为 $r_i$，

$\begin{aligned} I&=\sum\lambda\Delta r\cdot r_i^2 \\ &= \int_0^l \lambda r^2 {\rm d} r\\ &= \frac{1}{3}ml^2 \end{aligned}$

(2) 中心轴（质心轴）

同样的木棒，围绕其中心（质心）轴旋转，可看做两个小棍棒围绕端点旋转，并且其长度$l'=\frac{l}{2}$，易得

$I=\frac{1}{12}ml^2$

(3) 偏移中心的棍棒转动惯量

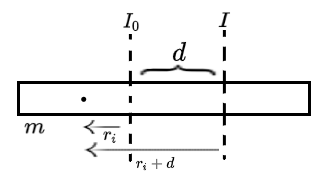
我们假设原先转轴的转动惯量为$I_0$，偏移转轴距离$d$后的转动惯量为$I$，棍棒质量为$m$，长度为$l$。我们从转轴向外积分可得：

$\begin{aligned} I_0&=\sum \Delta mr_i^2 \\ \end{aligned}$

$\begin{aligned} I&= \sum \Delta m(r_i+d)^2 \\ &= \sum \Delta m(r_i^2+2r_id+d^2)\\ &= I_0+d^2m+\sum(\Delta m\cdot 2r_id) \end{aligned}$

我们发现，当转轴取质心$C$时，$\sum(\Delta m\cdot 2r_id)=0$。所以对于任意一个转轴，与质心距离为$d$时，转动惯量

$I=I_C+d^2m$

这也被称作平行轴定理

3. 圆盘的转动惯量

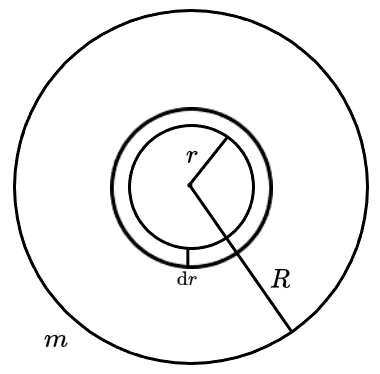
我们可以从中心往外积分

$\begin{aligned} I&=\sum \Delta mr^2 \\ &= \sum 2\pi r\Delta r\cdot\frac{m}{\pi R}r^2\\ &= \int_0^R \frac{2\pi m}{\pi R^2}r^3 {\rm d} r\\ &= \frac{1}{2}mR^2 \end{aligned}$

4. 薄球壳的转动惯量

从上往下把球壳看做圆环即可

设其面密度$\sigma=\frac{M}{4\pi R^2}$，极坐标角度为$\theta$，则其宽度为$R {\rm d}\theta$，面积$ds_i=2\pi R\sin\theta\cdot R{\rm d}\theta=2\pi R^2\sin\theta{\rm d}\theta$，圆环半径$r$为$R\sin\theta$

$\begin{aligned} I&=\int_0^\pi r^2{\rm d}m\\ &=\int R^2\sin^2\theta\cdot\sigma\cdot2\pi R\sin\theta{\rm d}\theta\\ &=2\pi\sigma R^4\int \sin^3\theta{\rm d}\theta\\ &=2\pi\sigma R^4\cdot\frac{4}{3}\\ &=\frac{2}{3}MR^2 \end{aligned}$

5. 球体的转动惯量

球体可以从球心向外积分，分成许多薄球壳。

设球的体密度$\rho=\frac{M}{\frac{4\pi R^3}{3} }=\frac{3M}{4\pi R^3}$。每一个球壳半径为$r$，厚度${\rm d}r$，体积$4\pi r^2{\rm d}r$

$\begin{aligned} I&=\int_0^R \frac{2}{3}r^2{\rm d}m\\ &=\frac{2}{3}\rho\int_0^R r^2{\rm d}V\\ &=\frac{2M}{R^3}\int_0^R r^4{\rm d}r\\ &=\frac{2}{5}MR^2 \end{aligned}$

转动惯量的例题

1. 小人击球（清华大学强基试题）

题目描述

（多选）手持球棒一端打击放置在底座上的球，击打过程中人的手可近似为不动。球棒质量为$1kg$，长$1.2m$，角速度为$10rad/s$，球的质量为$0.75kg$，则打出后球的速度可能为

A. $7.0m/s$

B. $6.5m/s$

C. $5.7m/s$

D. $5.3m/s$

答案

ABCD

解析

设球棒转动惯量为$I$，长度为$l=1.2m$，质量为$m=1kg$，球的速度为$v$，原角速度$\omega_0=10rad/s$，击打后的角速度为$\omega$，易得

$I\omega_0=I\omega+lmv$

最小值情况（最坏情况，球的恢复系数小）：

$l\omega=v$

最大值情况（过程能量守恒，没有损失）：

$\frac{1}{2}I\omega_0^2=\frac{1}{2}I\omega^2+\frac{1}{2}mv^2$

计算可得四个答案全部在数值范围内。

2. 轻杆吊球（深圳中学直升考试题）

题目描述

如图，有一绳子挂在天花板上的$A$点，绳子底端挂着一个轻杆$CD$，长$2l$，被绳子悬挂在中间$B$点，两侧悬挂着质量为$m$的球。$CD$点下方也挂着一根轻杆$EF$，长度也为$2l$，悬挂两根轻杆的绳子$CE$与$DF$均长$l$。现剪断$DF$处的绳子，请问在绳子被剪断的那一瞬间，绳子$AB$的拉力T为多少？

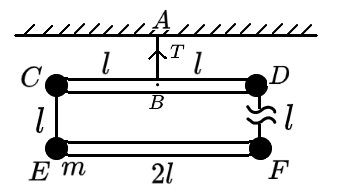
答案

$T=\frac{8}{3}mg$

解析

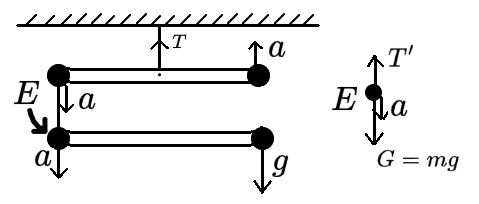
先分析四个球的加速度。

设$E$球受到绳子拉力为$T'$。对$E$球受力分析，易得

$G-T'=ma$

对$CBD$杆列角动量守恒。以$B$点为转轴，有

$lT'=2ml^2\frac{a}{l}$

（其中$lT'$为$C$点的角动量，$T'$是绳子上$E$点的反作用力。$C$球与$D$球的总转动惯量为$2ml^2$，而角加速度$\beta=\frac{a}{l}$是根据$v=\omega r$两侧对时间求导得来的）

解得$T=\frac{8}{3}mg$

3. 绳拽滚轴（清华大学强基试题改编）

题目描述

现有一线轴，其内外半径分别为$r$，$R$，该线轴的转动惯量为$I$。现以水平面向上$\theta$角大小为$F$的力拉这个线轴。请问：在$\theta$角为多少时，无论力$F$多大，都无法使得这个线轴为纯滚动？

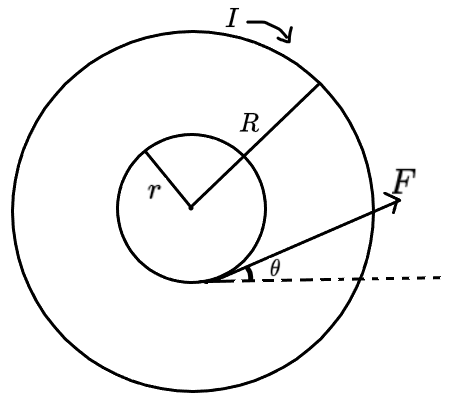
答案

$\theta=\arccos(\frac{r}{R})$

解析

从力，力矩，角速度三个方向列方程可得：

$\begin{cases} F\cos\theta-f=ma \\ -Fr+fR=I\beta \\ \beta R=a\quad(\omega R=v)\\ \end{cases}$

只需使得该方程无解即可。

解得 $\theta=\arccos(\frac{r}{R})$