题解 P8668 [蓝桥杯 2018 省 B] 螺旋折线

本蒟蒻写的第一篇题解，点个赞再走呗~

思路

当我们看到标签的时候，会看到这样两个字：“模拟”。

所以本蒟蒻的第一个方法就是模拟。

非常令人激动的是，最后四个点 TLE 了……

所以，我们要使出我们的终极大法：打表 找规律。

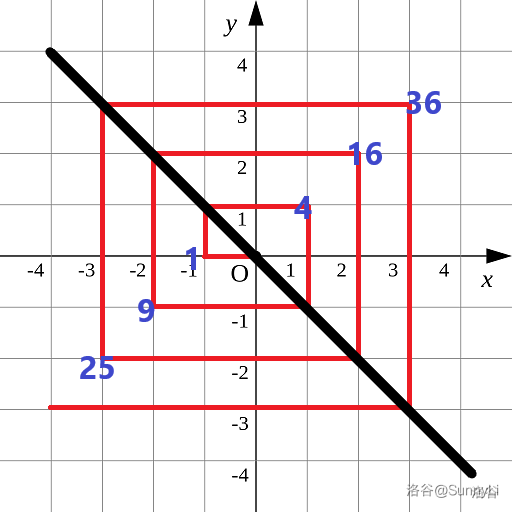
我们可以把它分为四个象限，求出顶角的 $dis$ 值，然后再加减坐标距离值 $dis(X,Y)$ 与顶点坐标的 $dis$ 值。

1. 第一象限

第一象限中，我们设 $m=\rm{max}(|x|,|y|)$ ，此时 $dis(m,m)=(2m)^2$ 。

接着需要判断 $x<m$ 或 $y<m$ 。

(1)当 $y=m$ 时，坐标 $(x,y)$ 在 $(m,m)$ 左侧，此时需要减去 $m-x$ ，即 $dis(x,y)=dis(m,m)-(m-x)$ 。

(2)当 $x=m$ 时，坐标 $(x,y)$ 在 $(m,m)$ 下边，此时需要加上 $m-y$ ，即 $dis(x,y)=dis(m,m)+(m-y)$ 。

2. 第二象限

第二象限中，坐标 $(m,m)$ 的 $dis(m,m)=2m(2m-1)$ 。但是此时 $x\in(-\infty,0]$ ，故 $x$ 需要取绝对值。

比较方法同上（或查看 AC 代码）。

3. 第四象限

第四象限中，坐标 $(m,m)$ 的 $dis(m,m)=2m(2m+1)$ 。但是此时 $y\in(-\infty,0]$ ，故 $y$ 需要取绝对值。

比较方法同上（或查看 AC 代码）。

4. 第三象限

第三象限的坐标的 $dis$ 值的规律本蒟蒻实在没想出来，所以用了第二和第四象限的坐标 $dis$ 值计算，此时需要判断 $|y|>|x|$

(1)当 $|y|>|x|$ 时，$dis(m,m)=2m(2m+1)$ ， 此时 $dis(x,y)=dis(x,y)+(m+|x|) $。

(2)当 $|y|<|x|$ 时，$dis(m,m)=2m(2m-1)$ ， 此时 $dis(x,y)=dis(x,y)-(m+|y|)$ 。

AC 代码

\\（可能不是最优解）
#include<bits/stdc++.h>
using namespace std;
typedef long long ll;

int main(){
    ll x,y,m,cnt,dis;
    cin >> x >> y;
    m = max(abs(x),abs(y));
    if(x>0 and y>=0){
    	dis = (m*2)*(m*2);
    	if(x<m)	dis -= (m-x);
    	else if(y<m)	dis += (m-y);
	}
	else if(x<=0 and y>0){
		dis = (m*2)*(m*2-1);
		if(abs(x)<m)	dis += (m-abs(x));
    	else if(y<m)	dis -= (m-y);
	}
	else if(x>=0 and y<0){
		dis = (m*2)*(m*2+1);
		if(x<m)	dis += (m-x);
    	else if(abs(y)<m)	dis -= (m-abs(y));
	}
	else if(x<0 and y<=0){
		if(abs(y)>=abs(x)){
			dis = (m*2)*(m*2+1);
			dis += (m+abs(x));
		}
		else{
			dis = (m*2)*(m*2-1);
			dis -= (m+abs(y));
		}
	}
	cout << dis;
    return 0;
}

AC 记录