浅谈我在对麦克斯韦方程组的理解

本文大致难度：高中

这篇文章的写作时间是本人新初二时学完高中电磁学后，认识了麦克斯韦方程组（仅仅只是看到了）后的一些看法，并且篇幅不长，如有问题欢迎评论区指出！

今天刚刚结束了高中电磁学的学习（交流电除外），正好又看到了有关麦克斯韦方程组的科普视频和文章，这里谈谈我的看法。

§ 麦克斯韦是谁？

以前看一些量子的科普书籍中有这个名字，事实上，他改变了我们对光的理解。事实上，爱因斯坦都是他的粉丝。

麦克斯韦实现了电磁学的统一，也由麦克斯韦方程组推出了光速，并且发现光是一种电磁波。

§ 关于麦克斯韦方程组

方程组共有四个公式，内容如下：

$\begin{cases} \displaystyle\oint E\cdot\mathrm{d}S=\frac{Q}{\varepsilon_0}\\ \displaystyle\oint B\cdot\mathrm{d}S=0\\ \displaystyle\oint E\cdot\mathrm{d}l=-\frac{\mathrm d}{\mathrm{d}t}\int B\cdot\mathrm{d}S\\ \displaystyle\oint B\cdot\mathrm{d}l=\mu_0I+\mu_0\varepsilon_0\frac{\mathrm d}{\mathrm{d}t}\int E\cdot\mathrm{d}S\\ \end{cases}$

如果你学过关于电磁学的部分内容，其实你应该感到非常眼熟。

1. 公式1（E·ds）

$\displaystyle\oint E\cdot\mathrm{d}S=\frac{Q}{\varepsilon_0}$

这就是静电场中非常著名的高斯定理。高斯定理是指一个封闭曲面中，封闭曲面内产生的电场对曲面内电通量的贡献为定值，只与内部电荷量的代数和有关。

这里举个小例子：有一根无限长的带电绳子，其电荷线密度为 $\lambda$，求电场的大小。

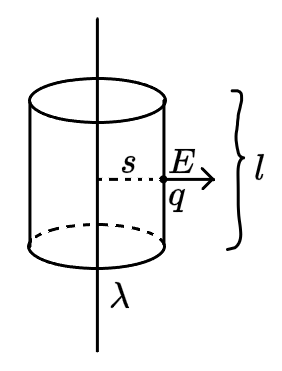
直接取一个圆柱形高斯面，而其上下两个圆形面并未有电场线穿过（擦过或者贴贴情况不算的哈），故只需考虑侧面。

$\begin{aligned} \oint E\cdot\mathrm{d}S&=E\cdot 2\pi sl=\frac{Q}{\varepsilon_0}=\frac{\lambda l}{\varepsilon_0}\\ &\Rightarrow E=\frac{\lambda}{2\pi s\varepsilon_0}=\frac{2k\lambda}{s}\\ \end{aligned}$

如果常规微元法也可以做，只是计算量稍微大了一点。

$\theta\in(-\frac{\pi}{2},\frac{\pi}{2})$

$\mathrm{d}l=\frac{s}{\cos^2\theta}\mathrm{d}\theta$

$\begin{aligned} F&=2\sum\frac{k(\Delta l\cdot\lambda)q\cos^2\theta}{s^2}\cdot\cos\theta\\ &=2\int_0^\frac{\pi}{2}\frac{k\frac{s}{\cos^2\theta}\mathrm{d}\theta \cdot\lambda \cdot q\cos^3\theta}{s^2}\\ &=2\int_0^\frac{\pi}{2}\frac{k\lambda q\cos\theta}{s}\mathrm{d}\theta\\ &=\frac{2k\lambda\cdot q}{s} \end{aligned}$

$E=\frac{F}{q}=\frac{2k\lambda}{s}$

2. 公式2（B·ds）

$\displaystyle\oint B\cdot\mathrm{d}S=0$

这个公式或许是四个公式中最好推的。由于磁场是无源场并且磁感线闭合的原因，通过一封闭曲面的磁感应强度必然为 $0$。

3. 公式3（E·dl）

$\displaystyle\oint E\cdot\mathrm{d}l=-\frac{\mathrm d}{\mathrm{d}t}\int B\cdot\mathrm{d}S$

如果你还没学电磁感应的话，或许这个公式会更眼熟：

$\displaystyle\oint E\cdot\mathrm{d}l=0$

上述等于 $0$ 的式子是对于静电场而言的，因为静电场是一个保守场，其电势的变化仅与其初末位置有关。

但是如果你学了电磁感应的话，你应该知道一个叫做感应电动势的东西：

$\varepsilon=\frac{\Delta\Phi}{\Delta t}$

这个公式告诉了我们一个结论：感生电动势的大小等于磁通量的变化率。

我们物理老师有一个说让我们要牢记于心的公式：

$E=-\frac{\partial\varphi}{\partial r}$

这个式子揭示了场强与电势之间的关系。所以说，$\displaystyle\int B\cdot\mathrm{d}S$ 就是感应电动势，而 $\displaystyle-\frac{\mathrm d}{\mathrm{d}t}\int B\cdot\mathrm{d}S$ 就是场强。

4. 公式4（B·dl）

$\displaystyle\oint B\cdot\mathrm{d}l=\mu_0I+\mu_0\varepsilon_0\frac{\mathrm d}{\mathrm{d}t}\oint E\cdot\mathrm{d}S$

这个公式是四个公式中最复杂的。有一个稳恒磁场中的简化形式：$\displaystyle\oint B\cdot\mathrm{d}l=\mu_0I$。这就是安培环路定理。

举个栗子：试求无限长直导线外一点的磁感应强度，其中导线电流 $I$，距离导线 $a$。

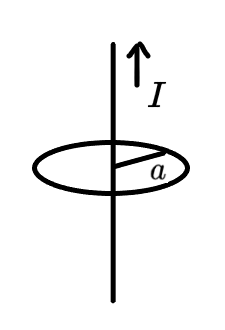
可以取一个半径为 $a$，垂直于导线且过该点的圆形环路，有

$\oint B\cdot\mathrm{d}l=\mu_0I\Rightarrow B\cdot2\pi a=\mu_oI\Rightarrow B=\frac{\mu_0I}{2\pi a}$

当然如果你用毕奥-萨伐尔定律积分的话也不是不行。

但是后面的一坨，就是麦克斯韦比较重要的发现了。

我们先举个栗子，如果说有一个静止的电荷，那么他只会产生电场。那么如果电荷运动了呢？直觉第一反应是同时会产生磁场，而事实上确实是这样的。

麦克斯韦发现，变化的电场同样产生了一个电流，其表达式为：

$\varepsilon_0\frac{\mathrm d}{\mathrm{d}t}\oint E\cdot\mathrm{d}S$

将这个数值代入其实际电流中，就有了最后一个方程式：

$\displaystyle\oint B\cdot\mathrm{d}l=\mu_0I+\mu_0\varepsilon_0\frac{\mathrm d}{\mathrm{d}t}\oint E\cdot\mathrm{d}S$

这也被叫做安培-麦克斯韦定律。

§ 总结一下

整个方程最后是非常令人惊艳的，这四个式子足以统一了电磁学，也表示了电磁学中的四个东西：电，磁，电生磁，磁生电。

也正是这个式子，让人们认识到光是一种电磁波，而且好巧不巧的是，光速 $\displaystyle c=\frac{1}{\sqrt{\mu_0\varepsilon_0}}$。

这是我第一次接触到这个方程，希望等到后面正式学起这个东西时，会有不同的认识。