§ 圆周运动的定义与公式
一个物体运动,如果其轨迹为圆周,我们则称之为圆周运动。
圆周运动主要分为两种:
- 匀速圆周运动:任何相等时间段内通过长度相等。
- 变速圆周运动:不是匀速圆周运动……
1. 角速度
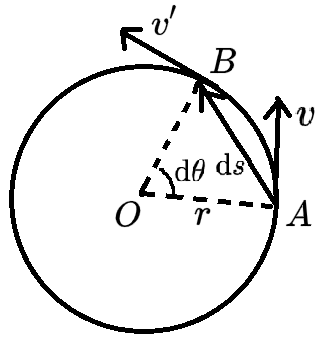
我们定义角速度 ω 为
ω=dtdθ(或ω=ΔtΔθ)
角速度可以描述质点圆周运动的快慢,ω 的方向可以由右手螺旋定则确定。
2. 线速度
v=dtds=dtdθ×r=ωr(或v=ΔtΔs)
3. 角加速度
β=dtdω
当质点做匀速圆周运动时,β=0;匀加速运动时,β 与 ω 同向;匀减速运动时,β 与 ω 反向;β 恒定的圆周运动称之为匀变速圆周运动,满足
ω=ω0+βt
θ=ω0t+21βt2
4. 线加速度
这是一个重头戏,大部分圆周运动的运动力学题目基本上都会有它的存在。我们先从线加速度引入。
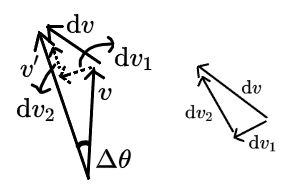
如图1,我们假设速度的变化
dv=v′−v
将 dv 分解为 dv1 和 ${\rm d}v_2 $,此时有
a=dtdv=dtdv1+dtdv2
其中,dv1/dt 是速度方向的变化快慢,dv2/dt 是速度大小的变化快慢,决定了圆周运动是匀速还是变速。
我们通常记 dv1/dt 为向心加速度,一般记作 an。记 dv2/dt 为切向加速度,一般记作 at(或者 aτ)。
我们所见到的大部分题目都是匀速圆周运动,故向心加速度的作用就变得非常大,所以向心加速度的计算公式就必不可少了。
an=rv2=ω2r
5. 向心加速度
(1) 推导过程
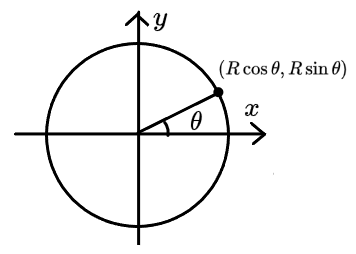
以圆周运动轨迹圆心为原点创建平面直角坐标系,我们可以用 θ 表示质点圆周运动所在的坐标,在 x 和 y 两个方向求出其加速度,最后勾股定理合成。
x=Rcosθ(θ=ωt)
vx=dtdx=−Rωsinθ
ax=dtdvx=−Rω2cosθ
y=Rsinθ
vy=dtdx=Rωcosθ
ay=dtdvy=−Rω2sinθ
所以
an=ax2+ay2=R2ω4cos2θ+R2ω4sin2θ=ω2R
(2) 向心力
现在,我们知道了 an 的表达式,我们就可以通过牛顿第二定律得出向心力的计算公式
F向=mrv2=mω2r=mωv
对于一般情况下的圆周运动,都有
F合=F向
即合外力提供向心力。
§ 圆周运动的模型
1. 圆锥摆
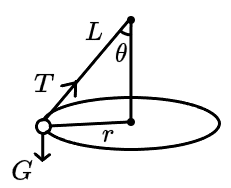
{F合=Tsinθ=mω2r=mω2LsinθTcosθ=mg
易得
ω=Lcosθg
2. 圆盘转动
圆盘转动时,两物体于同一轴转动,故角速度 ω 相同。
3. 传送带传动
此时线速度 v 相等。
§ 圆周运动的例题
1. 圆盘转动
题目
有两物体 A,B,距离转轴的距离分别为 l,2l 且处于转轴同一侧(如图)。A,B 之间有绳子连接,且质量均为 m。求绳子恰好有力时圆盘角速度的大小于 A,B 恰好不滑动时圆盘的角速度的大小(第一问考虑摩擦力,摩擦系数为 μ。第二问假设圆盘光滑,无摩擦力)。
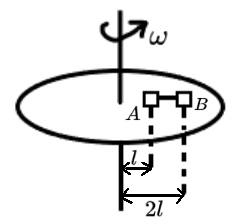
答案
μmg/2l ;2μg/3l
过程
{FA=mω2lFB=mω22l=μmg
解得 ω=μmg/2l
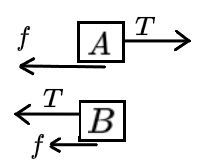
{f−T=mω2lT+f=mω2⋅2l
解得 ω=2μg/3l
2. 临界圆锥摆
题目
两绳系一个质量为 m=0.1kg 的小球,绳子另一端分别固定于一轴的 A,B 处,上方的绳子长 l=2m. 当绳子拉直时,绳子与轴的夹角分别为 30∘ 与 45∘ ,问球角速度为多少时两绳均有拉力?
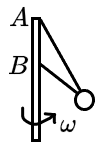
答案
3103<ω<10
过程
临界问题,求出两绳分别没有拉力时的角速度可得范围。
(1) TB=0 时,
{TAsin30∘=mω12⋅lsin30∘TAcos30∘=mg⇒ω1=3103
(2) TA=0 时,
{TBsin45∘=mω22⋅lsin30∘TBcos45∘=mg⇒ω2=10
易得 3103<ω<10
3. 类圆锥摆
题目
如图,长 L 绳一端系座椅,另一端固定于半径为 r 的水平转盘边缘。转盘可以绕穿其中心轴以角速度 ω 匀速转动。若此时绳子与转盘在同一平面运动,与竖直夹角 θ 时,求 ω 与 θ 的关系?

答案
ω=Lsinθ+rgtanθ
过程
列方程,有
mω2(Lsinθ+r)=mgtanθ
解得,ω=Lsinθ+rgtanθ
4. 半圆轨道
题目
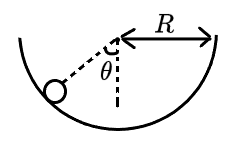
如图,一半球形小碗半径为 R,一质量为 m 的小球处于图示位置,重力加速度为 g,问:
(1) 小球禁止释放瞬间,求碗对小球的支持力与小球的加速度(计摩擦力)。
(2) 若小球以 v 的速度通过图示位置,求此时碗对小球的支持力与小球的加速度(不计摩擦力)。
答案
(1) N=mgcosθ;a=gsinθ−μgcosθ
(2) N=mgcosθ+mRv2;a=R2v4+g2sin2θ
过程
(1)
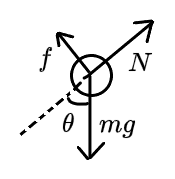
受力分析,有 N=mgcosθ
∴a=mF合=mmgsinθ−μmgcosθ=gsinθ−μgcosθ
(2)
mRv2=N−mgcosθ=ma⊥⇒N=mgcosθ+mRv2
ma∥=mgsinθ−f=mgsinθ−μmgcosθ−μmRv2
当 μ=0,有
a=a∥2+a⊥2=R2v4+g2sin2θ
5. 水漩涡
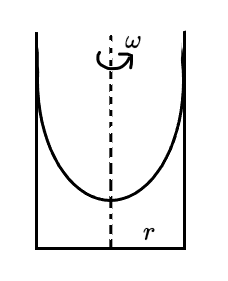
题目
现有一圆柱形水杯装了适量的水。现以角速度 ω 旋转水杯形成漩涡。试求漩涡的切面方程,其中重力加速度取 g。
答案
y=2gω2x2
过程
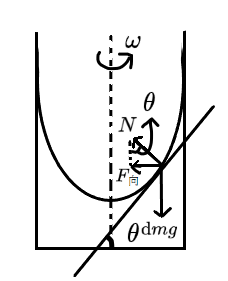
取一质量点 dm,有
dmgtanθ=dmω2x
又根据切线斜率 $\displaystyle \tan\theta=\frac











