§ 开普勒三大定律
1. 开普勒第一定律
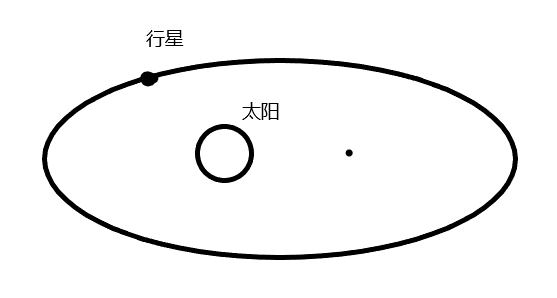
所有行星绕太阳转动的轨迹是椭圆,太阳处于一个焦点上。
2. 开普勒第二定律
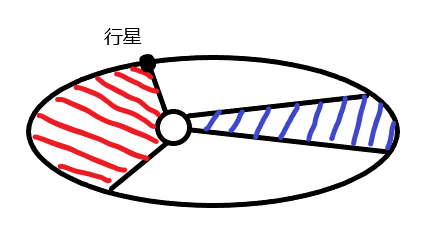
对任意一个行星来说,它与太阳的连线在相等的时间内扫过的面积相等。
事实上,有一个物理量与这个结论有一些关系,这里稍微提及一下。
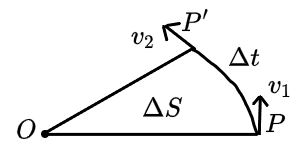
这个新物理量被称作面积速度,考虑一个质点 P 与一个固定的点 O 的连线在 P 点运动的过程中扫过的面积的快慢,这就是面积速度。面积速度一般记作 Av。平均面积速度的定义记作
Av=ΔtΔS
关于开普勒第二定律的证明,这里不详细多讲,总体来说可以总结为角动量守恒,即
M=dtdL=r×F=Fr⋅sin2π=0
3. 开普勒第三定律
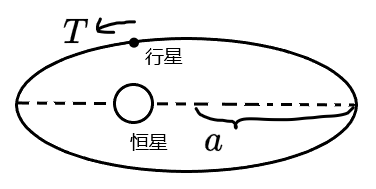
所有行星的轨道半长轴的三次方与它公转周期的平方的比值均相等,即 a3/T2=k,其中 a 为椭圆轨道半长轴,T 为公转周期, k 与中心天体有关,为一定常量。
由这个定律,可以推出来一些二级结论。这里讲一个比较常见的结论。
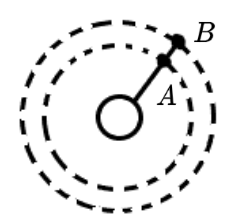
假设在同一星系中有两颗行星 A,B,角速度分别为 ωA,ωB,周期为 TA,TB,则两颗行星与太阳在同一条直线的周期满足
T=ωA−ωB2π=TB−TATATB
§ 万有引力定律
1. 定义式
F万=Gr2Mm
其中 G 为万有引力常数,经实验测量后得到 G=6.67×10−11 N⋅m2/kg2。这个公式适用于两个质点(或者均匀球体)之间。当然,物理中是少不了特殊情况的。
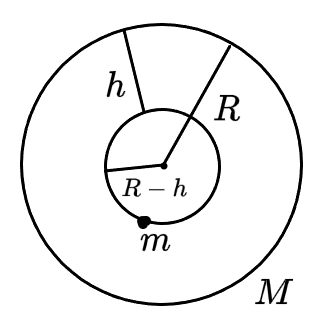
(1) 物体位于实心球内部
此时内部物体所受万有引力等效为内部球体的万有引力。即
F=G(R−h)2MR3(R−h)3m=GR3Mm(R−h)
(2) 物体处于球壳内
在球壳中,质点所受万有引力合力为 0。事实上,对于所有满足平方反比定律的公式(如库仑力)都有这样的结论。标准证明需要用到立体角的知识,这里用一种不太严谨的近似方法证明,感兴趣的可以去看看关于立体角证明,很多大学教材都有。
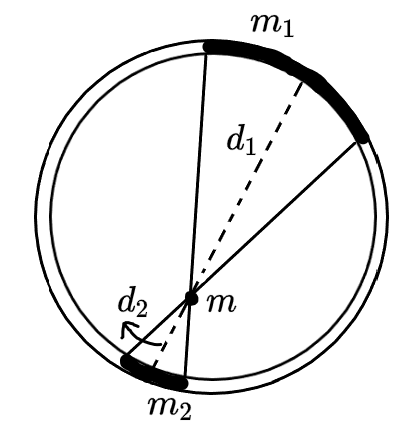
假设球壳的厚度非常小为 h≪R,其密度为 ρ。空间中有一质点 m,可得
m2m1=d22d12⇒d12Gm1m:d22Gm2m=1:1⇒合力为 0
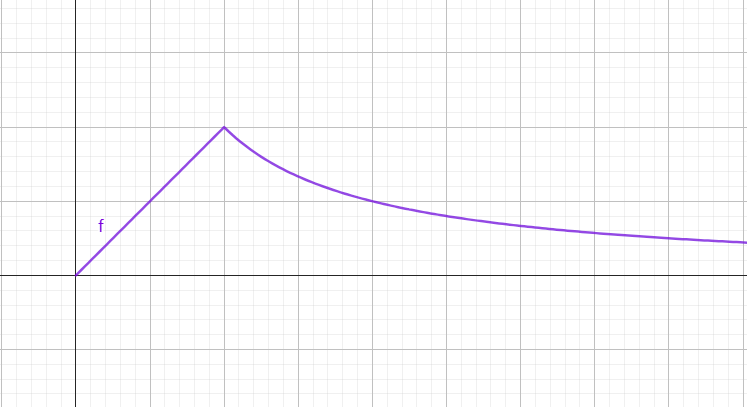
由上述两个结论可以画出从星体中心至无穷远处的 F−r 图像。
F={R3GMmr, 0<r≤Rr2GMm, r>R
2. 万有引力与重力
(1) 忽略自转
地表附近:
mg=GR2Mm⇒g=R2GM⇒gR2=GM
天上 h 处:
g′=(R+h)2GM=(R+hR)2g
(2) 考虑自转
极地:
mg=GR2Mm
赤道:
R2GMm=mg+mω2R
事实上,在星系星球级别的距离中,重力势能的公式有更精确的公式
W=∫F⋅ds=∫RR+H(R+h)2GMmd(R+h)=−R+hGMm∣∣∣∣RR+H=RGMm−R+HGMm
上面的推导是对于移动一个距离 H 的势能变化。对于一个点此处的引力势能,有
Ep=−GRMm
§ 航天问题
1. 卫星问题
- 近地卫星:r轨=r星,v 最大,T 最小。
- 同步卫星:(老教材只能在赤道上空)T=24h,r轨≈6r星。
- 极地卫星:经过两级,正对经线。
2. 环绕问题
卫星环绕,其中 F万 提供 F向,可以得出以下二级结论
v=rGMω=r3GMa=r2GMT=2πGMr3
你只需要按照 F万=F向⇒Gr2Mm=mrv2⇒v=rGM,其余同理可得。
3. 变轨问题
现假设有一卫星正在升高,在 P 点和 Q 点火,则有
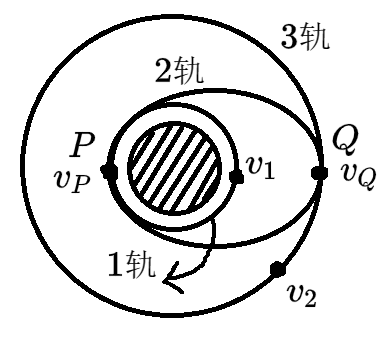
⎩⎪⎪⎪⎨⎪⎪⎪⎧vQ<v2<v1<vpaP=a1aQ=a2T1<T3<T2
或者总结为:v 变大时,有向心力大于万有引力,则做离心运动,轨道升高,v 再变小,反之亦然。
4. 中心天体的密度
ρ=34πR2M{给定g时,M=GR2g未给定g时,M=T2G4π2r3
5. 宇宙速度
- 第一宇宙速度:卫星绕地球,v1=RGM=gR=7.9 km/s。
- 第二宇宙速度:理论逃逸地球速度值,不考虑其他星体影响,可列能量守恒 21mv22−RGMm=0⇒v2=11.2 km/s。
- 第三宇宙速度:理论逃逸太阳系速度,v3=16.7 km/s。
§ 多星问题
本实例仅考虑双星运动。
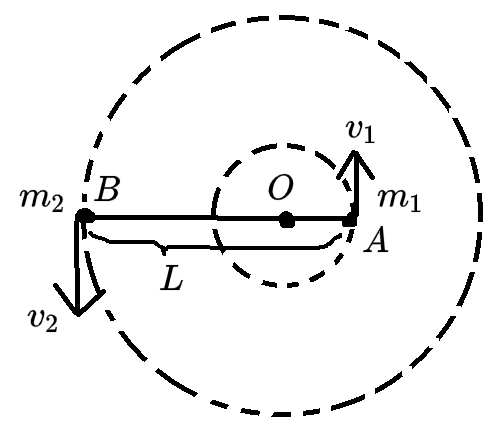
双星相互旋转可看作匀速圆周运动,其中万有引力提供向心力。围绕同一点运动,周期与角速度必然相等,有
GL2m1m2=m1r1v12=m1ω12r1GL2m1m2=m2r2v22=m2ω22r2
上式化简有
GM总=ω2L3rbra=mamb
§ 例题
1. 三星连珠
题目描述
已知某行星与地球绕着太阳公转,且地球半径小于行星半径,轨道均视为圆形。N 年三者共线一次,问行星与地球的公转半径之比?
答案
(N−1N)32
过程
⎩⎪⎨⎪⎧T地2r地3=T行2r行3N=ω地−ω行2π=T行−T地T地T行
解得
r地r行=3r地3r行3=(T地T行)32=(N−1N)32
2. 割补法
题目描述
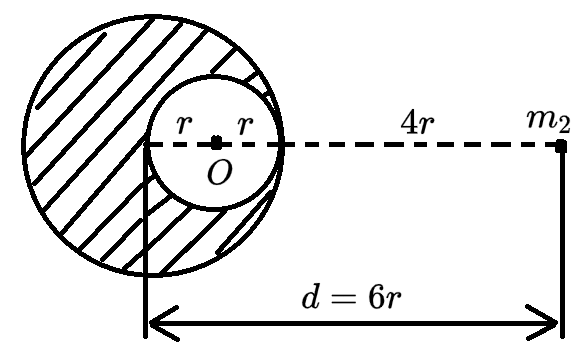
一质量分布均匀的球体,半径为 2r。在内部挖去一半径为 r 的空穴,表面与球相切。已知挖去部分质量为 m1,球心与空穴心连线,距离球心 d=6r 处有一个质量为 m2 的质点。问球体剩余部分对 m2 的万有引力有多大?
答案
225r241Gm1m2
过程
我们可以将这个不完整的球体补成完整的球体的等效引力减去质量为负的小球的等效引力。
F穴=G(5r)2m1m2=G25r2m1m2
F原=G(6r)28m1m2=G9r22m1m2
F剩=F原−F穴=225r241Gm1m2
3. 昼夜时长
题目描述
一绕地匀速卫星,其周期为近地卫星的 22 倍。已知地表重力加速度 g,地球半径 R。近似认为太阳为平行光。问卫星绕地一周有多长时间可被阳光照射?
答案
310πg2R
过程
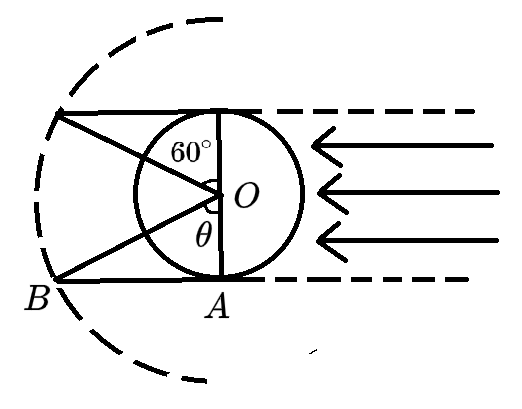
如图
OA=R,OB=4πg2R=2πgR2r3⇒r=2R
∴cosθ=1/2, θ=60∘
mg=mω2R=mT24π2R
∴T=2πGMr3=2πgR2R3=2πR/g
T′=4π2R/g
∴t=5T′/6=310πg2R
4. 横穿地球
题目描述
已知地心为 O,地球半径为 R,密度为 ρ。若取地心为零势能面,求一质量为 m 的物体位于距离地心为 r 的 P 点时所具有的势能,其中 r<R。
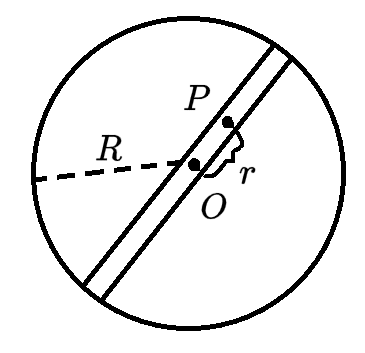
答案
Ep=32Gmπρr2
过程
Ep=∫0rF⋅dh=32Gmπρr2
5. 太空电梯
题目描述
现有一太空电梯,上端指向天空,下端接触地面但无相互作用力。电梯位于赤道处,与地球不存在相对运动。在只考虑地球对电梯的万有引力的情况下,试求电梯所能达到的最大长度。已知地球半径 R0=6370 km,地表重力加速度 g=9.8 m/s2,电梯质量视作均匀分布。
答案
144000 km
过程
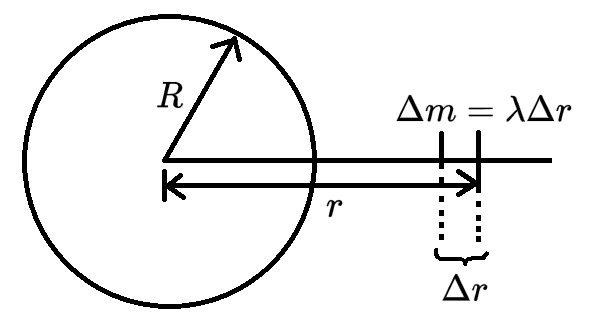
设太空电梯的线密度为 λ,则有
λ⋅Δr=Δm
尝试列能量守恒的式子
Ek=∫R0R0+lr2GMλdr=∫R0R0+lλω2r⋅dr=−r1GMλ∣∣∣∣R0R0+l=21r2λω2∣∣∣∣R0R0+l=21ω2(l2+2R0l)
故有
R0GM−R0+lGM=21ω2(l2+2R0l)
带入数值,解得 l=144000 km。













